A. Introduction
The Mathematics Curriculum for SS(S4-S6) is a continuation of the existing Mathematics curriculum at the junior level (S1- S3) and it is a core subject for the senior secondary level.
B. Overall Aims
1. To further develop students’ mathematical knowledge, skills and concepts.
2. To provide students with mathematical tools for their personal development and to further their career pathways.
3. To provide a foundation for students who may further their studies in Mathematics or other related areas.
4. To develop in students generic skills, and in particular, the ability to use mathematics to solve problems, give reasons and communicate with the others.
5. To develop in students an interest in and positive attitude towards mathematics learning.
6. To develop students competence in dealing with mathematics needed in life.
7. To help students to fulfil their potential in mathematics.
C. Framework of Curriculum
The structure of the curriculum for SS can be represented diagrammatically as follows:
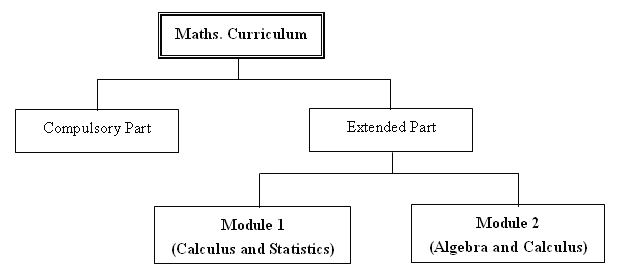
All SS students may have one of the following three options:-
1. Take the Compulsory Part only
2. Take the Compulsory Part with module 1 only.
3. Take the Compulsory Part with module 2 only.
D. Organization of Curriculum
1. Compulsory Part
(a) Course weight —- 10% to 12.5% of the total lesson time.
(b) Learning units :-
S4 topics(suggested)
—- Number System.
—- Quadratic equations.
—- Introduction of functions
—-Graph of quadratic functions and their graphs.
—- Equations of straight lines
—- Exponential and logarithmic functions.
—- More about equations
—- Trigonometric functions
—- Basic properties of circles
S5 topics(suggested)
—- Circles and tangents
—- More about inequalities
—- Applications of trigonometry in 2-dimensional problems
—- Locus and equation of circles
—- Variations
—- More about graphs of functions
—- Measures of dispersion
S6 topics(suggested)
—- Arithmetic and geometric sequences and their summations.
—- Llinear programming.
—- Use and abuses of statistics
—- Further applications
—- Inquiry and investigation
(c) Total learning time — 270 hours to 338 hours
2. Extended part
(a) Course weight —- 2.5% to 5 % of the total lesson time.
(b) Learning units:-
Module 1 (Calculus and Statistics)
S4 topics(suggested)
—- Binomial expansion
—- Exponential and logarithmic functions
—- Derivative of a function
—- Differentiation of a function
—- Second derivative of a function
—- Application of differentiation
S5 topics(suggested)
—- Indefinite integrals and its applications
—- Definite integrals and its applications
—- Approximation of definite integrals by trapezoidal rule
—- Conditional probability and independence
—- Bayes’s theorem
—- Discrete random variables
—- Probability distribution and expectation
—- Some discrete distributions and their applications
S6 topics(suggested)
—- Normal distribution and its applications
—- Sampling distribution and point estimates
—- Confidence interval for a population
—- Inquiry and investigation
Module 2 ( Algebra and Calculus )
S4 topics(suggested)
—- Surds
—- Mathematical induction
—- Binomial theorem
—- More about trigonometric functions
—- Introduction to the number ‘e’
—- Limits of functions
—- Differentiation
S5 topics(suggested)
—- Application of differentiation
—- Indefinite integrals and techniques of integration
—- Definite integrals and its applications
—- Determinants
—- Matrices
S6 topics(suggested)
—- System of linear equations
—- Introduction to vectors
—- Scalar product and vector product of vectors
—- Applications of vectors
—- Inquiry and investigation
E. Relationship between Mathematics(S1–3) Syllabus and SS Mathematics Curriculum
| Mathematics (S1 – S3) | SS Mathematics |
| Identities and Factorization Linear Equation in One Unknown More about Factorization |
Quadratic Equation |
| Introduction to Coordinates Coordinate Geometry |
Functions and Graphs |
| Law of Integral Indices | Exponential and Logarithmic Functions |
| Algebraic Expressions and Polynomials Identities and Factorization |
More about Polynomials |
| Rate and Ratio | Variation |
| Angle in Rectilinear Figures Congruent and Similar Triangles Theorems Related to Triangles Properties of Quadrilaterals |
Basic Properties of Circles |
| Introduction to Trigonometric Ratios Application of Trigonometry |
More about Trigonometry |
| Number Pattern Formulae |
Arithmetic and Geometric Sequence and their Summations |
| Linear Equation in Two Unknowns Inequality |
Inequalities and Linear Programming |
| Introduction to Coordinates Coordinate Geometry |
Equations of Straight lines and Circles |
| Introduction to Probability | More about Probability |
| Measure of Central Tendency | Measures of Dispersion |
| Use and Misuse of Statistics | Use and Abuses of Statistics |
F. Public assessment
All students who finish studying S6 will sit for a public examination called The
Hong Kong Diploma of Secondary Education(HKDSE). It provides a common
end-of-school credential that gives access to university study, work, further study
or other training.
The assessment arrangements in the public examination are outlined in the
following tables:
1. Compulsory Part
| Content | Weight | Duration | |
| Public Examination | Paper 1 Conventional questions Paper 2 Multiple choice |
65% 35% |
2 hrs 15 mins. |
2. Module 1 (Calculus and Statistics)
| Component | Weight | Duration | |
| Public Examination | Conventional questions | 100% | 2 hrs 30 mins. |
3. Module 2 (Algebra and Calculus)
| Component | Weight | Duration | |
| Public Examination | Conventional questions | 100% | 2 hrs 30 mins. |
Note. There will be no SBA for the above modules.
Finally, the HKDSE will make use of standards-referenced reporting assessment, which means that candidates’ level of performance will be reported with reference to a set of standards as defined by cut scores on the variable or scale for a given subject as follows:
Within the context of the HKDSE there will be five cut scores which will be used to distinguish five levels of performance with “5” being the highest. Performance below the threshold cut score of level 1 will be labeled as “ Unclassified” (U).
To maintain current levels of discrimination for selection purposes, some level 5 candidates with an outstanding performance will have their results annotated with the symbol ** or * and there will also be a Statement of Results which will provide additional level descriptors.
The levels awarded to candidates in the Extended Part will be reported separately from the Compulsory Part.

